|
|
|
About this capture | ||||||||||||||
La distance de Jeans en 2d
21 mai 2004
Ce problème de distance de Jeans a déjà été évoqué dans un dossier précédent. Plaçons-nous toujours dans un espace de calcul fermé. L'instabilité gravitationnelle se manifestera si la dimension caractéristique (par exemple le périmètre d'une sphère S3 dans un calcul en trois dimensions) est supérieur à une dimensions caractéristique appelée longueur de Jeans, qui fait intervenir la vitesse d'agitation thermique moyenne <C> de la population considérée ainsi que sa masse volumique r.
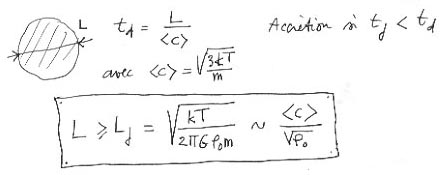
Que faire quand on calcule en 2d, c'est à dire sur une sphère S2 ? On peut s'attendre à quelque chose de similaire. Mais, justement, pour un calcul qui peut durer plusieurs heures, avec un nombre de points donnés, comment choisir la valeur des masses des points (donc la masse volumique) ainsi que celle de la vitesse d'agitation thermique moyenne <C> ? Il doit bien y avoir une "longueur de Jeans 2d" qui puisse se calculer avec ces données. Si elle est supérieure au périmètre de la sphère S2 il ne se passera ..rien. Pas de grumeaux, de "clusters" en vue. Inversement, si cette longueur caractéristique est faible devant ce périmètre on verra se former une multitude de condensations.
Comment sortir de cet empirisme"time-consuming" ?
Nous connaissons la dimension d'une force : M L T-2 . Appliquons cela à la force de gravité :
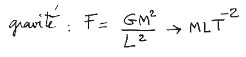
Nous faisons ici de l'analyse dimensionnelle (qui consiste à chercher "comment ceci varie en fonction de cela". Cette équation signifie simplement que si un système de masse M et de dimension caractéristique L évolue sous l'effet de forces de gravité, cette évolution se fera en un temps caractéristique obéissant à :
![]()
Si je me place en 3 dimensions :
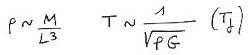
qui m'indique l'ordre de grandeur du temps caractéristique d'accrétion tj. J'ai déjà fait le calcul complet en 3d et obtenu :
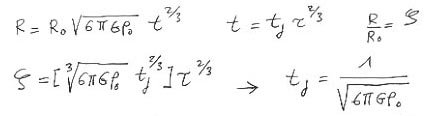
Il y a seulement un coefficient numérique qui se rajoute à ma formule. En 3d le calcul est facile car il y a un théorème qui me dit que le champ gravitationnel créé par une sphère de masse M, de densité constante et le même, à l'extérieure de celle-ci, y compris à son contact, que si tout cette masse était concentrée au centre de la sphère. J'obtiens alors une équations différentielle du seconde ordre (qui est d'ailleurs l'équation de Friedman) que je peux résoudre à la main et qui me donne le résultat ci-dessus.
En 2d il n'y a rien de ce genre. Si on prend une disque contenant de la matière, avec une " densité surfacique s " il n'y a pas de théorème équivalent. Le champ créé sur le cercle frontière n'est pas celui qu'on obtiendrait en concentrant toute la masse au centre du disque. C'est ... compliqué. Je vais donc me rabattre sur l'analyse dimensionnelle.
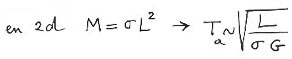
Il faudrait utiliser l'ordinateur pour déterminer le coefficient numérique qui doit se glisser dans cette formule.
Problème de similitude.
Mais une chose saute tout de suite aux yeux : le temps d'accrétion dépend cette fois de la taille du grumeau, ce qui n'était pas le cas en 3d. Ainsi on ne pourra pas tirer des conclusions péremptoires et définitives de toute simulation effectuée en 2d en affirmant "cela doit se passer de manière identique en 3d".Les études en 2d ne seront qu'indicatives. On est dans le qualitatif. Cela donne encore plus envie de savoir comment les choses se passent en 3d. C'est la raison pour laquelle nous attendrons avec une certaine impatience que le système à N machines, permettant de calculer avec un nombre de points suffisant soit opérationnel. Et là, ça ne dépend pas de moi. Tout est entre les mains de la bande d'informaticiens qui a décidé de relever ce défi.
A partir de ce temps caractéristique d'accrétion on peut construire l'ordre de grandeur d'une "distance de Jeans 2d".
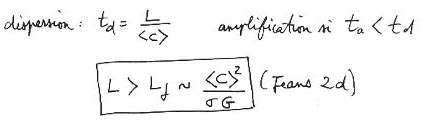
Là encore on voit que les choses sont différentes, par rapport à la formule en 3d. Cette distance caractéristique est très sensible à la vitesse d'agitation thermique, puisqu'elle croit comme son carré. Il faudrait que quelqu'un fasse un travail de simulation pour évaluer le coefficient numérique qui doit compléter la formule donnant le temps d'accrétion. J'avoue que je n'ai pas le savoir en programmation qui me permette de faire cela sur ma machine. J'ai écrit des programmes de CAO assez sophistiqués, mais c'était en Basic compilé et il y a 20 ans. J'ai par ailleurs fort à faire pour assurer la protection de mes travaux en Egyptologie, que j'avais envoyés à un congrès qui doit se tenir en septembre 2004, à Grenoble. Vous trouverez ci-après la réponse qui m'a été faite le président de ce IX° congrès international d'égyptologie :
|
Grenoble, le 9 mai 2004 Monsieur, Je suis au regret de vous informer de ce que le
Comité Scientifique, saisi de votre demande de présentation
d'une communication au IX° Congrès n'a pu la prendre en considération.
En raison du nombre important de participants et du fait que vous n'êtes
ni membre de l'Association Internationale des Egyptologues ni non plus
d'une instance universitaire ou de recherche habilitée, de Comité
se voit dans l'obligation d'écarter les candidatures extérieures.
|
J'avais envoyé cet article, rédigé dans les formes et parfaitement clair, à une revue de publication spécialisée, où je me heurte à la même surdité. Celle-ci ne m'a d'ailleurs même pas adressé en retour d'accusé de réception, assorti d'un numéro d'enregistrement, ce qui ne m'est jamais arrivé dans ma carrière de chercheur. Tout cela a une drôle d'allure. Mon expérience du monde de la recherche m'a souvent appris qu'hostilité et incorrection allaient souvent de pair. Il ne s'agit pas des quelques idées que j'ai mises sur mon site, concernant la navigation hauturière dans la Haute Antiquité. Disons que si un pharaon me demandait s'il me serait possible de diriger pour lui la construction une pyramide de 145 mètres de haut, en utilisant uniquement du bois, des cordes, les outils de l'époque et la force des hommes, avec en outre une précision centimétrique, je pourrais lui répondre par l'affirmative, ayant résolu tous les problèmes lés à cette tâche. Etant données la simplicité et la clarté des solution proposées, parfaitement fonctionnelles, j'ai été étonné de voir cet article de 25 pages refusé à ce colloque, en invoquant non des arguments d'ordre scientifique, mais des raisons d'ordre administratif. Je vais donc devoir accélérer la publication de "Peter Small découvre le secrets de la construction des Grandes Pyramides" pour prendre de vitesse des gens qui auraient pu trouver quelque inspiration dans mes écrits.
Retour vers l'archive Projet Epistemotron