Quelques idées pour un logiciel

22 mai 2004

Depuis le début de l'opération Epistémotron un certain nombre d'entre vous ont créé leur propre programme de simulation 2d sur sphère S2. Mon souhait le plus vif serait de pouvoir présenter un de ces logiciels sur mon site en permettant aux lecteurs-néophytes de se faire la main avec. Comme nous l'avons défini dès le départ, cette stratégie passe par la mise à disposition des codes-sources.

Je n'ai pas suivi les débats sur la liste SIMTOILE, faute de temps. Il faut avant tout que ces logiciels que vous créez soient "ergonomiques", d'abord simple, évident, même. Mettez vous à la place d'un type qui débarque. Il n'aura fait au mieux que de lire ces textes en diagonale. Il télécharge le logiciel. Il faut, très vite, qu'il accroche, sinon il zapera.

Il se trouve que j'ai une certaine expérience de la programmation, ayant écrit dans les années quatre vingt des logiciels de CAO (Pangraphe, Superpangraphe, Screen) assez volumineux, qui tournèrent sur Apple II E, puis Amstrad 6128 et Mac Intosh. A cette époque, sur d'aussi petits systèmes j'avais un modeleur assez puissant et élaboré et je pouvais produire des images avec parties cachées éliminées. Ces images ont été produites par Screen dont j'avais vendu 1500 exemplaires par correspondance il y a vingt ans. Ci après, le modèle central du "retournement du cube", une version polyédrique du retournement de la sphère.

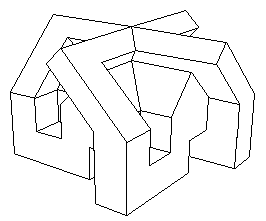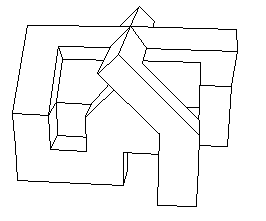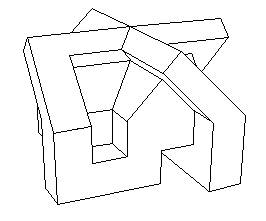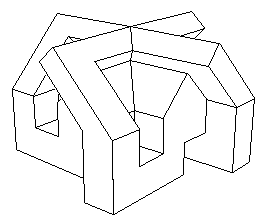
A cette époque un logiciel de CAO était un truc inextricable, fort cher, associé à un manuel de plusieurs centaines de pages. Il fallait avoir avalé cent pages minimum pour être capable de créer et de gérer un simple cube. Mon logiciel ... n'avait pas de manuel. J'avais rendu son utilisation évidente. C'est ce que je souhaiterais vous voir faire ici et je vais donner quelques idées de base dans ce but.

Il y a plusieurs problèmes :

- L'introduction des données

- Le contrôle du calcul

- La visualisation du travail en cours.

Dans un programme il y a une boucle dans laquelle la machine interroge l'état de la souris et du clavier en répercutant les ordres. Je ne connais pas les langages actuels de programmation mais j'imagine que, conceptuellement du moins, les choses n'ont pas dû beaucoup changer. Jadis il existait un registre qui contenant, sous forme alphanumérique, le code de la dernière touche frappée. Selon la valeur en question un sous-programme correspondant était activé. Aujourd'hui la souris existe (dont l'utilisation ne fut intégrée que dans mon logiciel de CAO SCREEN). Mais il ne faut pas sous-estimer la commodité de la commande par pression des touches, au clavier. Il faut que ces commandes soient les plus simples possibles. Il ne faut qu'un ordre corresponde à des choses aussi compliquées que Ctrl Alt Sup K .....

Ce qui suit ne sont que des suggestions. Quand vous créez un exécutable, en cliquant sur l'icône vous êtes tout de suite dedans. Mettez vous à la place du type qui débarque et qui n'a évidemment rien lu. Il lui faut tout de suite quelque chose à voir, à comprendre, pour l'accrocher. Mon ami Gilles a utilisé le format rectangulaire de l'écran pour mettre les commandes à gauche et l'aspect visuel à droite. Mettez vous dans la peau d'un lecteur qui débarque. Au hasard des clics il a atterri dans la zone "Epistémotron". Il voit "programme exécutable", clique et se retrouve face à quelque chose, sur l'écran. Ce quelque chose peut lui permettre de lancer des simulations passionnantes qui pourront durer une nuit entière et dont il pourra apprécier le résultat au matin. Mais d'entrée de jeu il lui faut quelque chose d'immédiat, de visuel, qui attire le regard.

Je suggère que sur la partie visuelle de l'écran on place une démo en gif animé, en boucle, "quelque chose qui en jette". Cela peut être la formation d'un cluster sur la sphère. Pensez à bien choisir les couleurs, pour que ça soit bien visible. Je pense que le contour apparent de la sphère devrait être matérialisé par un cercle.

Donc, quand le "client" lance l'exécutable, la première chose qu'il voit c'est, à droite, un écran où il voit quelque chose d'intrigant. A gauche le nom du programme avec un très court descriptif. Autant donner un nom générique à cet ensemble de programmes, pour que ça se grave dans la tête des gens. Je mettrais :

 

EPISTEMOTRON

Conception : J.P.PETIT

Mise en forme de cette version : Jacques Dupont

Version 2.1 25 mai 2004

   Ce programme vise à vous familiariser avec les grands problèmes de l'astrophysique, à travers des simulations numériques que vous réaliserez vous-même. Avec ce logiciel vous pourrez créer des systèmes planétaires, des amas d'étoiles, des galaxies (avec leur structure spirale), en tant qu'ensembles de N points-masses liés par la force de gravitation (on parlera de "systèmes auto-gravitants". Le calcul s'effectue sur une surface, en 2d. Cette surface, notre "espace de calcul" est une simple sphère, ce qui est une astuce pour "refermer l'espace" (les ordinateurs ne gèrent pas les espaces infinis). La force newtonienne variera comme l'inverse du carré de la distance curviligne, sur la sphère.
  A droite, vous pouvez observer le comportement de 1600 points-masses qui forment un "grumeaux" de matière, qu'on appellera aussi "clusters" (mot anglais qui signifie "grappes"). Mais avant de faire des choses de ce genre il faut vous familiariser avec l'outil.

Cliquez ici pour passer à la suite (bouton)

 

 


Manifestation de l'instabilité gravitationnelle dans un ensemble de 1600 "points-masses" évoluant sur une sphère. En s'attirant, les points forment une "condensation" ou cluster

(Gif animé en boucle)

 

Il faut concevoir l'EPISTEMOTRON comme un PROGICIEL, ayant une vocation pédagogique. Mais il n'y aura aucune différente entre le programme orienté recherche et ce progiciel. Ceux qui seront plus avancés sauteront simplement cette mise en main. Il suffit par exemple de mettre sur un onglet, en haut "si vous êtes plus avancés", onglet qui proposera des tâches déjà plus élaborées. Mais, pour le moment, restons dans la section progiciel. A chaque étape, à gauche, la description de commandes et à droite, le résultat immédiatement visible. Les gens ne comprendrons pas tout, tout de suite. Dites-vous "qu'ils débarquent" et ne savent rien. Il faut donc pratiquer la technique des "petites bouchées" et leur permettre à tout moment de pouvoir revenir à l'étape antérieure.

En bas, des démarches associées à des boutons :

Initiation          (bouton) étape précédente         (bouton) étape suivante

L'initiation comportera un certain nombre d'étapes. Le client pourra à volonté en cliquant se resituer l'une l'une quelconque de ces étapes, sur laquelle il voudra revenir.

On suppose que le type a cliqué sur ce premier bouton. Il est alors passé à l'étape suivante. Voici ce qu'il voit sur son écran.

 

EPISTEMOTRON

Votre espace de calcul

 

C'est une sphère où on a représenté méridiens et parallèles, de même que l'équateur et un des pôles. Les commandes :

Flèche (à droite, à gauche, eh haut, en bas) et
Shift Flèche (idem, plus fin)

Vous permettent de faire virevolter cette sphère. En pressant sur la touche Z vous activerez l'options zoom qui se pilote avec Flèche en haut, Flèche en bas.
En pressant une deuxième fois sur la touche Z vous annulez cette commande et vous revenez au pilotage angulaire de votre espace de calcul.

La touche C vous permet de changer le mode de présentation de votre espace de calcul.

La touche Q vous permet à tout moment de (Q)uitter le programme.

 

 
Azimut : 28°              Site : + 37°         Zoom : 1

 

Initiation          (bouton) étape précédente         (bouton) étape suivante

 

Ceci est ce que voit le lecteur avant qu'il n'ait touché à quoi que ce soit (touche ou souris). Dès qu'il touche à quelque chose, les inscriptions qui accompagnent la sphère disparaissant. Mais l'utilisateur pourra les faire réapparaître en activant le bouton "étape précédente". Ce système sera général.

Dès qu'il a pressé sur une touche les ensembles

- Flèches

- Shift Flèches

- Touche Z

- Touche C

- Evidemment à tout moment touche Q

deviennent actifs. Avec les flèches l'utilisateur fait tourner la sphère en tous sens, rapidement ou finement. Il serait opportun de faire figurer parallèles et azimut avec un pas de 10°. Un champ de 10° carré correspondra à une sorte de zoom tel que l'espace soit alors "quasi plat".

En pressant sur Z l'utilisateur passe en mode zoom, qu'il pilote avec les touches fléchées, haut et bas, pour "avant", "arrière". Les nombres affichés : azimut, site, zoom permettent de se resituer rapidement en un point donné de la sphère. Mais c'est juste pour le repérage. Il faut en règle générale éviter toute saisie numérique au clavier, dans le style "indiquez l'angle en azimut".

L'utilisateur moyen ne sait pas ce que sont un site et un azimut.

En pressant plusieurs fois sur la touche C(hanger) on change le mode d'affichage, cycliquement. cela peut être sur fond blanc, avec un contour apparent de sphère noir; ou sur fond noir avec ce contour apparent en blanc. On peut faire disparaître l'ensemble méridiens-parallèles ou le faire réapparaître à volonté. En fait cet ensemble n'est là que pour se situer rapidement (par rapport aux "pôles", à l'équateur et à un "méridien zéro", que j'ai oublié d'indiquer ici). On obtiendrait ainsi le cycle

- Méridiens-parallèles sur fond blanc
- Fond blanc mais système de cartographie enlevé
- Méridiens-parallèles sur fond noir
- Idem avec système de cartographie enlevé.

Voici par exemple l'une de ces présentations.

 

EPISTEMOTRON

Votre espace de calcul

 

C'est une sphère où on a représenté méridiens et parallèles, de même que l'équateur et un des pôles. Les commandes :

Flèche (à droite, à gauche, eh haut, en bas) et
Shift Flèche (idem, plus fin)

Vous permettent de faire virevolter cette sphère. En pressant sur la touche Z vous activerez l'options zoom qui se pilote avec Flèche en haut, Flèche en bas.
En pressant une deuxième fois sur la touche Z vous annulez cette commande et vous revenez au pilotage angulaire de votre espace de calcul.

La touche C vous permet de changer le mode de présentation de votre espace de calcul.

La touche Q vous permet à tout moment de (Q)uitter le programme.

 

 
Azimut : 28°              Site : + 37°         Zoom : 1

 

Initiation          (bouton) étape précédente         (bouton) étape suivante


Ca suffit pour l'apprentissage de la manipulation de l'espace. Il faut maintenant familiariser l'utilisateur avec le mouvement "libre" d'un point masse sur la sphère, selon une géodésique, c'est à dire un "grand cercle". Il faudra des commandes

M pour masse.

On suppose que l'utilisateur, ayant bien joué avec l'espace de calcul, aura pressé sur :

 (bouton) étape suivante

Il aura toujours sous les yeux l'espace de calcul, sous l'angle qu'il aura choisi et avec le niveau de zoom qu'il aura également choisi. Sur cet espace de calcul il pourra poser des points masses, un pour commencer. Mais s'il estime que l'angle de vision n'est pas bon, il peut à tout moment se servir du zoom. Il n'y a pas de manuel à lire préalablement. C'est le "tout à l'écran", systématique, en situation d'apprentissage. Voici l'écran suivant :

 

 

EPISTEMOTRON

Positionner un point, définir son vecteur-vitesse

En pressant sur la touche P vous signifiez que vous entendez poser un point-masse sur la sphère. Celui-ci apparaîtra (couleur) au centre du cercle-contour apparent. Vous le déplacerez avec les touches fléchées.

En appuyant sur M vous définirez la masse, +1 par défaut. Les touches Flèche en haut et flèche en bas modifieront la valeur de la masse, en passant éventuellement à des valeurs négatives. En plaçant la souris sur la masse, si celle-ci est "perçue", sa valeur apparaîtra dans une fenêtre. En cliquant, en déplaçant la souris puis en lâchant vous définirez le vecteur vitesse. La surface de la tache est proportionnelle à la masse, la longueur du segment à la vitesse.

La touche G(O) déclenche le mouvement.

La touche S(TOP) l'interrompt.

Le curseur qui est à droite permet d'obtenir un effet de ralenti.

 
Azimut : 28°              Site : + 37°         Zoom : 1

Masse : + 3      Vitesse : 5

 

Initiation          (bouton) étape précédente         (bouton) étape suivante

En appuyant sur la touche G l'utilisateur déclenche le mouvement (Go ! ). Je ne sais pas s'il est possible, à ce stade, de faire figurer la portion de trajectoire se situant sur le second hémisphère. Pointillé ? couleur atténuée ? Autre couleur, moins visible ? Comme la machine n'est occupée qu'à une seule chose : gérer le mouvement de cet unique point-masse, le mouvement ne sera pas perceptible. Apparaîtra la trajectoire : un grand cercle vu sous l'aspect d'une ellipse.

Après avoir pressé la touche G :

 

EPISTEMOTRON

Trajectoire géodésique (Grand Cercle)

En pressant sur la touche P vous signifiez que vous entendez poser un point-masse sur la sphère. Celui-ci apparaîtra (couleur) au centre du cercle-contour apparent. Vous le déplacerez avec les touches fléchées.

En appuyant sur M vous définirez la masse, +1 par défaut. Les touches Flèche en haut et flèche en bas modifieront la valeur de la masse, en passant éventuellement à des valeurs négatives. En plaçant la souris sur la masse, si celle-ci est "perçue", sa valeur apparaîtra dans une fenêtre. En cliquant, en déplaçant la souris puis en lâchant vous définirez le vecteur vitesse. La surface de la tache est proportionnelle à la masse, la longueur du segment à la vitesse.

La touche G(O) déclenche le mouvement.

La touche S(TOP) l'interrompt.

Le curseur qui est à droite permet d'obtenir un effet de ralenti.

 
Azimut : 28°              Site : + 37°         Zoom : 1

Masse : + 3      Vitesse : 5

 

Initiation          (bouton) étape précédente         (bouton) étape suivante

L'utilisateur comprend que la trajectoire d'un point matériel libre, animé d'une vitesse V s'inscrit, sur la sphère, sous l'aspect d'un Grand Cercle. Il va pouvoir réduire cette vitesse apparente en utilisant le curseur "ralenti".En Haut c'est 100 % de la vitesse. En bas : zéro pour cent. Il y aura toujours une position où le point se déplacera de manière satisfaisante pour l'oeil. Là, il y a un gadget à mettre au point, pour un faible nombre de points, qui évite d'encombrer l'écran avec le tracé des trajectoires. Il faut voir le point-masse (disque bleu), son vecteur vitesse (trait rouge) et son "sillage". L'effet de sillage pourra être obtenu en créant un effet de pointillé de plus en plus prononcé vers l'aval, jusqu'à effacement de la trajectoire. On peut ainsi donner un effet de "queue de comète". C'est d'ailleurs le système qui est utilisé sur les écrans de visualisation des radars de tir sur les chasseurs de nuit.

Après utilisation du curseur créant le ralenti :

 

EPISTEMOTRON

Trajectoire géodésique (Grand Cercle)

En pressant sur la touche M vous signifiez que vous entendez poser un point-masse sur la sphère. Celui-ci apparaîtra (couleur) au centre du cercle-contour apparent. Vous le déplacerez avec les touches fléchées.

Vous définirez la masse, +1 par défaut. Les touches Flèche en haut et flèche en bas modifieront la valeur de la masse, en passant éventuellement à des valeurs négatives. Shift F pour varier de 0.1
En plaçant la souris sur la masse, si celle-ci est "perçue", sa valeur apparaîtra dans une fenêtre. En cliquant, en déplaçant la souris puis en lâchant vous définirez le vecteur vitesse. La surface de la tache est proportionnelle à la masse, la longueur du segment à la vitesse.

La touche G(O) déclenche le mouvement.

La touche S(TOP) l'interrompt.

Le curseur qui est à droite permet d'obtenir un effet de ralenti.

 
Azimut : 28°              Site : + 37°         Zoom : 1

Masse : + 3      Vitesse : 5

 

Initiation          (bouton) étape précédente         (bouton) étape suivante

On peut toujours créer un objet à vitesse nulle en cliquant deux fois sur le point-masse (d'où un vecteur-vitesse de longueur nulle).

En pointant sur une masse avec la souris et en cliquant on fait aussitôt apparaître sa valeur. On peut la modifier avec les touches fléchées et shift fléchées. Si on veut mettre une masse négative on passera par la valeur zéro. Si cette valeur n'est que brièvement affichée, cela sera sans conséquence mais si on l'affiche plus d'une seconde cela signifiera qu'on entend faire disparaître cette masse et c'est ce qui se passera.

A l'écran on affichera des pastilles dont l'aire sera proportionnelle à la masse (ou au log de la masse, si on veut faire interagir des masses très dissemblables).

Quand le lecteur aura bien compris l'allure de la trajectoire il pourra passer à l'étape suivante.

 

 

EPISTEMOTRON

Deux corps en interaction

La touche F vous permet de fixer un point doté d'une masse M > 0

Vous pourrez alors en placer un second, avec masse m > 0 et vecteur vitesse et observer sa trajectoire (celle d'une comète ou d'un planète autour du Soleil). Vous pourrez ainsi espérer visualiser la trajectoires Keplériennes. Mais l'espace dans lequel vos points se meuvent est courbe, il n'est "quasi-plat" que sur de courtes distance, négligeables devant le périmètre de la sphère. Si ça n'est pas le cas vous observerez un phénomène de précession du périhélie, conforme à un mouvement dans un espace courbe (précession du périhélie de Mercure)

 
Azimut : 28°              Site : + 37°         Zoom : 1

 

Initiation          (bouton) étape précédente         (bouton) étape suivante

 

 

EPISTEMOTRON

Deux corps en interaction

Ce mouvement de précession deviendra négligeable si la trajectoire s'inscrit sur une portion de sphère faible devant l'aire de la sphère (utilisez le zoom).

 
Azimut : 28°              Site : + 37°         Zoom : 7

 

Initiation          (bouton) étape précédente         (bouton) étape suivante

 

 

EPISTEMOTRON

Deux corps en interaction

A tout moment vous pouvez interrompre le calcul à l'aide de la touche S(TOP). En pointant la souris sur une masse elle vous affiche aussitôt sa valeur et le module de sa vitesse. Avec les touches Flèche ou Shift Flèche vous pouvez modifier la valeur et le signe des masses. Restez avec effet de Zoom important pour être en "quasi-plat". Vous pouvez ainsi étudier les trajectoires d'une masse m > 0 repoussée par une masse
M < 0 . Vous découvrez au passage la dynamique ce ce système :

- Les masses de même signe s'attirent

- Les masses de signes contraires se repoussent

 
Azimut : 28°              Site : + 37°         Zoom : 7

 

Initiation          (bouton) étape précédente         (bouton) étape suivante

 

EPISTEMOTRON

Deux corps en interaction

En pointant à l'aide de la souris sur la masse fixée à l'aide de la commande F vous pouvez libérer celle-ci et observer, toujours en "quasi-plat" un mouvement où les deux corps orbitent autour de leur centre de gravité commun (s'ils s'attirent, bien sûr !).

 
Azimut : 28°              Site : + 37°         Zoom : 7

 

Initiation          (bouton) étape précédente         (bouton) étape suivante

L'idéal serait, bien sûr, qu'un lecteur concrétise tout cela sous forme de programme et que les dessins d'illustration puissent être remplacés par des copies d'écran, assortis de gif animés.

Autre gadget intéressant : quand, avant de lancer le calcul à l'aide de la touche G(O) on pointe une des masses avec la souris et clique, non seulement la masse et la vitesse s'affichent, mais le lecteur peut suivre en temps réel l'évolution de la vitesse de l'objet pointé.

 

EPISTEMOTRON

Deux corps en interaction

Effet de Fronde

Il faut pour cela tirer un objet léger vers un objet beaucoup plus lourd, lui-même en mouvement, comme s'il voulait le rattraper. En ayant cliqué sur l'objet léger avant de lancer le calcul à l'aide de la touche G on pourra voir s'afficher sa vitesse et le gain acquis par cet effet de Fronde.

 
Azimut : 28°              Site : + 37°         Zoom : 7

Masse : 1         Vitesse : 1.5


 

Initiation          (bouton) étape précédente         (bouton) étape suivante

 

EPISTEMOTRON

Deux corps en interaction

Effet de Fronde

Il faut pour cela tirer un objet léger vers un objet beaucoup plus lourd, lui-même en mouvement, comme s'il voulait le rattraper. En ayant cliqué sur l'objet léger avant de lancer le calcul à l'aide de la touche G on pourra voir s'afficher sa vitesse et le gain acquis par cet effet de Fronde.

 
Azimut : 28°              Site : + 37°         Zoom : 7

Masse : 1         Vitesse : 3.2


 

Initiation          (bouton) étape précédente         (bouton) étape suivante

 

 

EPISTEMOTRON

N corps en interaction (maximum : 100)

Evaporation d'un amas ouvert

Seuls les systèmes à deux corps sont stables. Les systèmes à plus de deux corps sont instables, surtout si les masses sont très dissemblables. Créez des systèmes à plusieurs corps suffisamment auto-attractifs. Vous pourrez jouer sur les masses et les vitesses. En pressant la touche V, en la maintenant enfoncée puis en utilisant les touches Flèche en haut - Flèche en bas vous pourrez modifier toutes les vitesses de votre système.

En Maintenant pressée la touche M et en utilisant les touches fléchées vous pourrez de la même façon modifier toutes les masses.

Après plusieurs essais vous obtiendrez un "amas ouvert" qui perdurera. Mais observez la façon dont l'amas éjecte alors les objets légers par effet de fronde.

NB : Si on pointe un objet et qu'on annule sa masse il "disparaît".

 
Azimut : 28°              Site : + 37°         Zoom : 7


 

Initiation          (bouton) étape précédente         (bouton) étape suivante

Dans la page htm l'illustration devrait être faite à l'aide d'un gif animé.

 

EPISTEMOTRON

Effet de lentille gravitationnelle

Revenez en zoom 1, avec la sphère plein cadre et les effets de courbure. Quand des photons cheminent dans un espace courbe tout se passe comme s'ils étaient attirés par les masses, gravitationnellement (leur masse est nulle, mais pas leur énergie, qui contribue, peu le savent, au champ gravitationnel général, pour une très faible part).

Nous ne représenterons pas la masse qui est "censée avoir courbé l'espace de cette façon". Mais nous étudierons la propagation de deux objets (ici, des photons) cheminant selon des géodésiques.

On prendra deux photons auxquels on donnera une masse la plus faible possible (mais non-nulle, sinon ces objets "disparaîtraient"). On les lancera avec des vitesses élevées. Les deux grands cercles décrits évoqueront l'effet de lentille gravitationnelle.

 
Azimut : 28°              Site : + 37°         Zoom : 1


 

Initiation          (bouton) étape précédente         (bouton) étape suivante

Si quelqu'un pouvait concrétiser ces idées sous la forme d'un logiciel-progiciel on pourrait le mettre sur le site en téléchargeable. Je pense que ce "produit" intéresserait les gens, que l'impact du projet Epistémotron s'en trouverait accrue et que ces gens seraient alors curieux de voir apparaître la suite, c'est à dire un logiciel où ils pourraient manipuler un grand nombre de points-masses, de masses positives et négatives, donc de participer activement à cette recherche collective.

Dans tous les cas de figure il faut garder en tête le souci d'ergonomie. Comme vous avez pu le voir dans cette simulation de logiciel (mais qui reste parfaitement réalisable) il n'y a pas de manuel à lire au préalable. A un moment où à un autre on pourra voir apparaître la description d'une commande T qui fera simplement apparaître sur la partie gauche de l'écran les différentes commandes-clavier et leur effet. En pressant une seconde fois sur cette touche T on reviendra au travail en cours.

Quand on passera à un système à plusieurs populations, figurées par des couleurs différentes, l'information clé sera la valeur de la distance de Jeans 2d qui apparaîtra sous la forme d'un segment coloré en bas de la fenêtre de droite. Quand la longueur de la fenêtre excédera celle de la fenêtre ce sous système sera gravitationnellement stable, tout simplement.

 

Retour vers l'archive Projet Epistemotron