Untitled Document

May	JUN	Aug
	18
2003	2004	2006

11 captures

18 Jun 2004 - 17 Jun 2008

About this capture

Prenons une sphère emplie de "poussières" c'est à dire d'une densité constante de points masses immobiles. La sphère a un rayon R. Elle représente une masse M. Considérons une masse m située à la surface de cette sphère. Ecrivons la loi de Newton. On obtient, en deux lignes de calcul, l'équation de Friedman, celle des modèles cosmologiques du même nom:

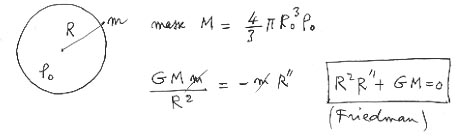
Vous pourrez retrouver les trois types de solutions de cette équadif du second ordre, qui donne les modèles :

En 1934 Milne et Mac Crea montrèrent que l'équations maîtresse de la RG pouvait émerger du newtonien. Dans les années soixante dix j'avais fait de même avec la solution mawellienne de l'équation de Boltzmann, couplée à l'équation de Poisson. Passons...

On va rendre cette équation adimensionnelle en iontroduisant une dimension caractéristique qui sera simplement la valeur initiale du rayon. Apparaît alors un temps caractéristique.

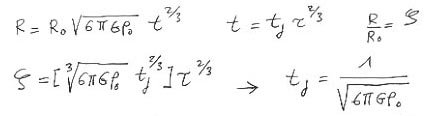
Si la solution d'Einstein de Sitter décrit une expansion ralentie, à partir de conditions initiales .. explosives, elle est symétrique en changeant t en - t . On obtient deux paraboles symétrique par rapport à un temps t = 0, évidemment arbitraire. Si on "lit" la courbe de gauche on a donc la description d'un collapse gravitationnel, qui s'auto accélère.

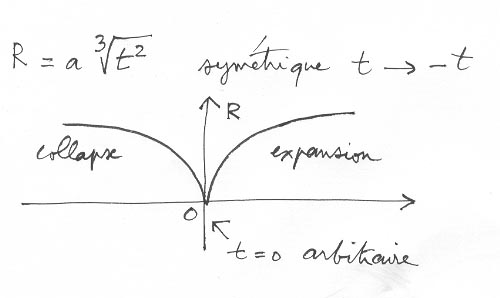
A ce phénomène se trouve associé ce temps caractéristique qu'on appelle le temps de Jeans. On voit donc qu'une masse de poussières (ensemble de particules dénuées de vitesse d'agitation), quelle que soit son envergure 2R implose en un temps qui ne dépend que de la valeur de la densité .

On va considérer maintenant le phénomène inverse : un nuage de masses m, de dimension L, qui est le siège d'un mouvement d'agitation thermique. On néglige les forces de gravité. Le nuage va se disperser en un temps caractéristique égal à L , divisé par la la valeur moyenne de la vitesse d'agitation thermique < C > , liée à la température absolue T (voir dossier précédent, sur la théorie cinétique des gaz). On appelera ce temps de dispersion t_d . Dans une sphère de gaz les deux phénomènes seront antagonistes. On s'aperçoit alors que le temps de dispersion est supérieur au temps caractéristique d'implosion, ou d'accrétion si simplement l'envergure du "grumeau" considéré excède une certaine longueur caractéristique, la Longueur de Jeans Lj

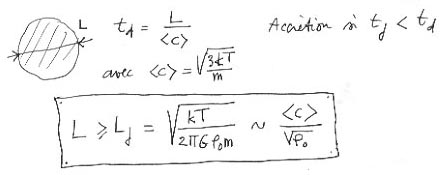
Celle-ci est proportionnelle à la vitesse d'agitation thermique < C > et inversement proportionnelle à la racine carrée de la densité r. Ainsi "si on chauffe, on stabilise".

- Qu'est-ce qui chauffe (par exemple une masse de gaz interstellaire). Réponse : les étoiles chaudes, émettant de l'UV.

- Qu'est-ce qui refroidit ? Les pertes radiative (le gaz rayonne de l'infra-rouge).

Une masse de gaz interstellaire fonctionne alors comme une chasse d'eau, est me siège d'un phénomène homéostatique. Si le gaz se refroidit (radiativement) il devient gravitationnellement instable et donne naissance à des étoiles qui, crachant de l'UV, le réchauffent et le regonflent. C'est un mécanisme "anti-dépression". Le phénomène stellaire joue vis à vis du gaz le rôle d'un anti-dépresseur. Ce gaz, dans une galaxie spirale, est confiné dans un disque très plat, de quelques centaines d'années-lumière d'épaisseur, ce qui est faible par rapport aux 100.000 années lumière qui représente le diamètre de la galaxie. La couche de gaz a la géométrie d'un disque microsillon. Elle est d'épaisseur constante, simplement parce que cette épaisseur est régulée par le même phénomène anti-dépression, partout.

Certains d'entre vous ont essayé de modéliser par simulation une instabilité gravitationnelle, sans succès. Parce que leur gaz était trop chaud, ou que les points masses n'étaient pas assez massifs. Ainsi la distance de Jeans était-elle supérieure au diamètre de leur grumeau initial; Il se passe un phénomène analogie en 2d, quand on travaille sur une sphère, ce que certains d'entre vous on fait. Vous pourrez vous amuser à construire l'équivalent de la théorie de Jeans, en 2d. On trouvera alors une longueur caractéristique qui sera proportionnelle à la vitesse d'agitation thermique 2d, sur la "peau" de cette sphère. La densité jouera un rôle analogue qu'en 3d, mais j'avoue que ce soir j'ai la flemme d'éclaircir ce problème, sans intérêt réel, puisque l'univers est 3d et non 2d. Mais qualitativemlent les phénomènes sont similaires. On devrait alors tomber sur une longueur de Jeans 2d. Si celle-ci est supérieure au périmètre d'un grand cercle de la sphère, pas de grumeaux. Si cette longueur de Jeans est petite devant ce périmètre : plein de grumeaux. Quand vous aurez en main les programmes de calcul sur la sphère 2d vous pourrez vous amuser avec cela. D'Agostini a fait un super-programme que j'installerai dans le dossier suivant. Vous aurez à la fois l'exécutable et le code source, pour bricoler. C'est en Pascal.

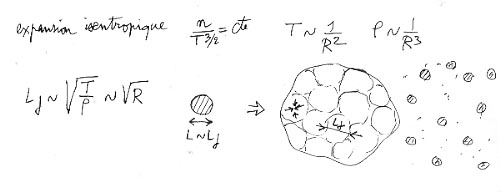
On voit que la longueur de Jeans croît en racine de R. Donc fatalement un truc qui est en expansion isentropique devient instable, se fragmente. S'il n'y avait pas eu les photons, le rayonnement cosmologique, l'univers aurait créé des grumeaux dès son plus jeune âge. Or il se trouve que le couplage matière rayonnement a inhibé l'instabilité gravitationnelle jusqu'à ce que l'univers se désionise vers t = 100.000 ans. Si on prend alors la vitesse d'agitation thermique d'hydrogène qui est juste en dessous de 3000°, et la densité qui régnait à l'époque on trouver une certaine valeur de la longueur de Jeans, et si on calcule la masse qui se trouvait dans ces grumeaux on trouve la masse de Jeans associée qui à l'époque avoisinait les 100.000 masses solaires. Donc il est logique de penser qu'au moment du découplage ce seraient des masses équivalentes à celle des amas globulaires qui se seraient constituées en grumeaux séparés.

Une petite remarque pour finir. Quand je suis arrivé à l'observatoire de Marseille, je fuyais une abominable galère qui était l'Institut de Mécanique des Fluides (alias "laboratoire de ploutomécanique"). Le labo, qui était à côté de l'actuelle gare des cars à Marseille, près de la gare de chemin de fer de Saint Charles, a été rasé il y a quelques années. Son directeur est six pieds sous terre. C'est là que j'avais annihilé l'instabilité de Vélikhov en 1966, ce qui avait fait naître bien des fièvres. Un jour, assis devant mon générateur MHD impulsionnel en forme de canon à gaz je m'étais dit "mec, si tu fous pas le camp d'ici, tu vas devenir comme les autres". J'avais alors avalé en quelques mois un traité de théorie cinétique des gaz, le "Chapman et Cowling", intitulé "The mathematical theory of non uniform gases", Cambridge university press. Un excellent ouvrage dont je ne saurais trop recommander la lecture et qui initiera ceux qui voudront aller plus loin dans la théorie avec le calcul à l'aide de dyades, de matrices dyadiques. En phase de digestion j'avais eu une ou deux idées et construit une thèse de doctorat - canot de sauvetage. Ce travail plut au mathématicien André Lichnérowicz, rencontré par hasard en train de siroter une menthe à l'eau dans un café d'Aix en provence. Sa protection m'évita de subir les foudres mandarinales et de quitter cette galère, pour atterrir hélas aussitôt dans une autre : le Laboratoire de Dynamique des Systèmes Réactifs. Un jour je me suis dit "cherchons un endroit calme". J'ai fait une étude et conclu que ce qui ressemblait le plus à une maison de retraite c'était l'observatoire de Marseille (à l'époque). J'ai alors, dans l'équation de Boltzmann rajouté la gravité, transformé mes électrons en étoiles, couplé tout ça à l'équation de Poisson, et roule Marcel. Six mois plus tard je m'amusais ferme avec les galaxies et autres trucs du plus haut cosmique.

J'ai commencé par trouver une bizarre équation. A l'époque les gens de l'obs étaient tous des observateurs et non des théoriciens. Ils étaient excellents pour concevoir des télescopes, tailler des miroirs. Mais pour la théorie, zéro. Guy Monnet était alors directeur (à l'époque il portait uen barbichette, sous le menton, qui le faisait ressembler à un personnage d'un roman de Jules Vernes). On m'envoya consulter un homme connu pour sa science, un nommé Hénon (pas du genre hilarant). Il regarda mes papiers et déclara "C'est l'équation de Jeans". Bon... j'avais retrouvé l'équation de Jeans, à partir de la théorie cinétique des gaz (je ne vous embêterai pas avec ça). Après j'ai fait de même en faisant émerger l'équation de Friedman. Au lieu d'apprendre l'astro et la cosmo, je réinventais. C'est excellent, d'ailleurs. On comprend mieux.

Dans ce qui précède j'ai mis assez d'éléments pour que vous compreniez ce que vous aurez sous les yeux, dans les simulations. Au passage nous étudierons le comportement de mélanges de matière et de matière gémellaire. On parlera alors d'instabilités gravitationnelles conjointes. J'ai présenté ça dans un congrès international d'astrophysique. Mais je crois que personne n'a rien compris. De toute façon, maintenant, les capacités intellectuelles d'un théoricien se chiffrent en gigalfops, gigatrucs et gigamachins.

Tout cela, ça va nous servir. Mais sans un poil de théorie pure derrière on pédale vite dans la giga semoule.