Untitled Document

Nous avons évoqué ailleurs des simulations sur des sphères 2d et des projets d'extension sur des sphères S3. Tout ce qui va suivre se réfère à des systèmes planétaires et peut donc se gérer dans un espace de calcul tridimensionnel euclidien, dans " R3 ". Si un objet quitte le système par effet de fronde, ça fait partie du jeu, des aléas de la vie planétaire. Beaucoup d'objets ont été éjectés hors du système solaore, au moment de sa création, par effet de fronde et ne sont jamais revenus.

Le système solaire recèle beaucoup de mystères. On ne sait pas comment il s'est formé. On ne sait pas "pourquoi il est dans cet état, avec tant d'aspects singuliers" et on ne sait pas non plus vers quoi il tend, ni ce qui va arriver dans un futur proche ou lointain. Tout cela peut être exploré dans le cadre du projet Epistémotron, et même dès à présent. Pour ce faire il faut diposer :

En voici. Ces astres se sont constitués sous l'effet de la force de gravitation. Il faut donc se donner des points-masses qui s'attirent selon la loi de Newton. Mais les planètes ne sont pas des objets totalement gazeux. Quand on s'enfonce dans Jupiter on trouve un état gazeux, puis cent kilomètres plus bas, liquide, puis solide et même ... métallique. Les anomalies de gravité suggéreraient même que des planètes géantes comme Jupiter et Saturne puissent digérer dans leurs entrailles une planète "tellurique", avalée à une époque indéterminée.

Comment se créer un système sphéroïdal qui garde sa cohésion sous l'effet de la force de gravité mais refuse d'imploser sous l'effet de forces répulsives ? Réponse : en introduisant une force :

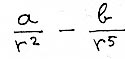
Pourquoi cette puissance 5 ? La section efficace de collision (voir chapitre sur la théorie cinétique des gaz) est une intégrale :

Accessoirement, quand la force est newtonienne, celle-ci ... diverge, ce qui implique de créer un "cut off". Je ne vais pas vous ennuyez avec cela, nous n'en aurons pas besoin. Plus tard, si le projet Epistémontron se développe et que nous envisagerons des phénomènes impliquant des "plasmas autogravitants" avec comme applications les quasars. Lisez ou relisez "On a perdu la moitié de l'univers" (Hachette, collection Pluriel). Toutes les idées qui sont là-dedans se prètent à des simulations. Je crois, que j'aurais eu de quoi faire travailler un bon paquet d'étudiants de la section "Sciences de l'Univers" du Cnrs. Mais le temps n'est plus à ces stratégies universitaires. Trop compliqué, trop lent, trop lourd. Laissons les potiches sur leurs étagères. Si les choses se passent comme je l'espère, ces idées sortiront de leur boite de Pandore et iront essaimer à travers le globe.

J'ai d'ailleurs toujours pensé une chose et je l'ai écrit dans un de mes premiers bouquins : ce ne sont pas les chercheurs qui s'emparent des idées, mais au contraire les idées qui s'emparent des chercheurs. Si le "greffon" prend, tout ira assez vite. Ce qu'on peut conjecturer c'est que les astrophysiciens (et les planétologues) seront probablement les derniers à réagir. Ma foi, si ça se passe ainsi, tant pis pour eux. Mais revenons à cette loi en 1/r⁵ . La section efficace est en principe variable selon la vitesse ( relative) des deux objets que l'on fait interagir. On a :

On pourra définir une valeur moyenne < Q > qui sera en général très voisine de Q ( < C > ). La particularité de la loi en1/r5 est que la section efficace ne dépend alors pas de la vitesse. Elle se prête ainsi très bien à un modèle dit "des boules de billard". La loi de force proposée ci-dessus évoque donc la dynamique de boules de billard tenues ensemble par la force de gravitation. Au lecteur de tenter de définir les paramètres a et b . C'est un terrain vierge où tout est alors question de feeling. Selon les choix, on pourra fabriquer une espèce d'étoile où la densité croît au fur et à mesure qu'on s'enfonce vers le centre ou une sorte de "goutte liquide", voir un solide assez visqueux, avec une densité à peu près constante partout. Conditions initiales : mettre les N points selon une distribution shérique, à densité constante, puis lâcher le tout. Ca peut osciller. Il est même possible de simuler une dissipation d'énergie en annulant toute vitesse d'agitation thermique des particules situées en surface, ce qui simulerait le refroidissement par émission d'infrarouge. On peut même alors converger vers une "planète froide", du style Lune.

Dans un système de calcul partagé il y a là matière à de multiples investigations. On peut même reproduire les courants de convection, la ... tectonique des plaques. En créant une injection d'énergie à coeur on peut simuler le fonctionnement d'une étoile (voire même l'explosion d'une supernova) comme on peut simuler le maintien en température par le dégagement d'énergie lié à la décomposition des radio-éléments.

Parmi les phénomènes qui nous intéressent il en est un, assez passionnant : l'effet de marée. C'est simple. Quand vous aurez recréé votre "planète", approchez une masse ponctuelle M. Celle-ci devrait se déformer en prenant la forme d'un ellipsoïde allongé. C'est le réglage de vos paramètres a et b qui conditionnera la "réponse" de votre planète, ou de votre étoile vis à vis d'une telle solicitation. Et c'est là qu'on tombe sur une des multiples idées de Souriau. Voir son travail de planétologie que je présente dans mon site, qui n'a jamais été publié ! Ne vous trompez pas : le grand spécialiste de planétologie en France, ça n'est pas André Brahic, c'est Jean-Marie Souriau. Le second prendra sa place dans l'histoire des sciences. Pour le premier, cela me paraît moins probable.

Si vous n'allez pas jeter un oeil sur ces pages, quelques mots. Le point de départ de Souriau est l'analyse des périodes des orbites des différentes planètes. Il retient alors celle de la Terre : 365 jours et celle de Vénus : 225 jours et calcule, à la fois vers l'aval et vers l'amont la suite de Fibonacci correspondante (ou du type de Fibonacci, où tout terme est la somme de deux qui le précèdent). On sait que dans ces conditions le rapport de deux nombres successifs de cette suite tend vers le nombre d'or.

Intervient alors le concept de résonance. Prenez un instrument à corde. Dans n'importe quel collège vous aurez la possibilité de mesurer la fréquence de deux cordes. Appelons T₁ et T₂ les périodes de ces fréquences propres. Si le rapport est l'unité et que vous pinciez l'une des cordes, la réponse de la seconde sera maximale. Elle restera acceptable si le rapport de ces périodes est

Réglez ensuite la tension d'une des cordes de manière à ce que ce rapport soit proche d'un nombre rirrationnel comme

Vous verrez l'effet de résonance s'effondrer. Il sera minimal si le rapport est égal au nombre d'or :

Prenez deux planètes comme le couple Neptune-Pluton. Le rapport de leurs "années" est proche de

Souriau en déduit que les deux orbites de Neptune et de Pluton vont s'influencer mutuellement. Mais comment ? Selon lui c'est le Soleil qui sert de "résonateur". Chaque planète crée à sa surface un effet de marée. Si vous constituez votre modèle d'objet sphéroïdal et si vous voulez que son comportement se rapproche de celui du Soleil il faudra qu'une planète comme Saturne soulève sa surface d'un centimètre. Vous devrez vérifier au passage que votre effet de marée varie en 1/r3 , ce qui fait que l'effet de marée créé par cette planète devra être comparable à celui du minuscule Mercure, mais qui est plus près de l'étoile solaire.

Limitez votre sytème solaire à la triade Soleil - Neptune - Pluton. Laissez mijoter un certain temps, comme disait fernand Reynand. Les simulations numériques permettent ce genre de chose. Les orbites vont se modifier et tendre vers un rapport où l'échange énergétique sera minimal, c'est à dire vers 1,6180...

Du moins c'est ce que nous conjecturons. Une intéressante expérience de calcul.

Les planétologues alignent les âneries en négligeant purement et simplement les phénomènes dissipatifs dans leurs calculs, alors qu'ils sont évidemment présents. C'est ainsi que vous avez pu lire des conclusions assénées par les "chaotiques". Mais, dixit Souriau :

la théorie du Chaos n'intègre pas les processus dissipatifs, qui sont la clé de la constitution et de l'évolution des systèmes planétaires.

Avec des systèmes à N corps bien configurés, intégrant les effets de marée et les processus dissipatifs il y a moyen de mettre en évidence de tas de choses. On peut créer un tableau :

Planète	Masse	Vitesse sur orbite	Distance au Soleil	Moment cinétique
Mercure	0,005 M_T soit 3 10²² k	4,789 10⁴ m/s	0,387 UA soit 5,76 10¹⁰ m	8,27 10³⁶
Vénus	0,815 M_Tsoit 4,87 10²⁴	3,5 10⁴ m/s	0,723 UA soit 1,1 10¹¹ m	1,87 10⁴⁰
Terre	5,98 10²⁴ k = M_T	2,98 10⁴ m/s	1 UA = 1,49 10¹¹ m	2,65 10⁴⁰
Mars	0,107 M_T soit 6,4 10²³ k	2,414 10⁴ m/s	1,524 UA soit 2,27 10¹¹ m	3,9 10³⁹
Jupiter	317 M_T soit 1,9 10²⁷	1,306 10⁴ m/s	5,2 UA soit 7,75 10¹¹ m	1,92 10⁴²
Saturne	92,2 M_T soit 5,51 10²⁷ k	9,64 103 m/s	9,55 UA soit 1,43 10¹² m	7,59 10⁴²
Uranus	14,5 M_T soit 8,67 10²⁵	6,81 10³ m/s	19,22 UA soit 2,86 10¹²	1,72 10⁴²
Pluton	0,002 M_T (?) soit 1,2 10²²	4,74 10³ m/s	39,4 UA soit 5,9 10¹² m	3,35 10³⁹

- Masse du Soleil : 2 10³⁰ k
- Rayon : 7 10⁸ m. Périphérie : 4,4 10⁹ m
- Période de rotation sidérale : 25 jours à l'équateur soit 2,16 10⁶ sec
- Vitesse en périphérie : 2037 m/s
- MRV = 2,85 10⁴²

Je ne me rappelle plus quelle est la valeur du moment cinétique d'une sphère de densité constante. &&& Je compte sur un lecteur pour m'envoyer cela. En mettant toute la masse du Soleil en bout de rayon on a une limite supérieure, qui est inférieure au moment cinétique des planètes géantes. Une question émerge : comment se forme le plan de l'écliptique ? On peut alors se donner une soleil constitué par N points-masses liés par la loi proposée (ou une loi dérivée, simulant les effets de marée). On place les 8 planètes sur des orbites circulaires situées dans des plans quelconque. On dote le Soleil d'un axe de rotation quelconque. Chaque planète va créer un effet de marée sur le Soleil. C'est lui qui sert "d'antenne" vis à vis de la force de gravitation. Une première conjecture consiste à imaginer qu'un plan de l'écliptique va alors se former, par le simple jeu des effets de marée et que ce sont les planètes géantes qui mèneront le jeu, et non le Soleil. On peut même conjecturer que le Soleil verrait son axe se redresser, de manière à se placer perpendiculairement à ce plan de l'écliptique. Une étude intéressante.

Si on dispose d'assez de points-masses, liés par la loi de force ad hoc, on peut modéliser tous les astres. On peut même simuler les processus dissipatifs en annulant périodiquement toute vitesse d'agitation des points en surface. Une telle machinerie numérique pourrait permettre de reconstituer toute l'histoire de la constitution du système solaire, avec non seulement création du plan de l'écliptique mais circularisation des orbites. L'idée générale est que le système Soleil plus planètes se met de lui-même dans un état de résonance minimal. C'est l'idée de Souriau. Des simulations en calcul partagé devraient permettre de donner corps à ces idées. La partie délicate est la simulation de la dissipation. Tout cela n'est pas simple car au moment où le système solaire se constitue les magmas des jeunes planètes doivent être encore fluides et ce milieu doit être l'objet de courants de convection. Il est aussi vraisemblable que beaucoup de choses se produisent dans la foulée. Les planètes accroissent leurs masses en dévorant ce qui se trouve sur leur passage. Inversement, elles éjectent par effet de fronde, soit carrément hors du système solaire, soit dans sa grande banlieue les petits objets qui deviendront les futures comètes et astéroïdes. Tout cela doit être amusant en diable à simuler.

Personnellement, le fait que le moment cinétique du système solaire soit principalement détenu par les planètes extérieures me laisse à penser que celui-ci pourrait avoir été acquis lors de collisions entre proto-systèmes planétaires (étoiles en formation, plus disques de gaz et de poussières, tenus à distance par la pression de radiation). C'est le modèle "des oeufs sur le plat en trois dimensions". C'est par un mécanisme similaire que les galaxies spirales acquièrent, à mon sens, le mouvement de rotation qui affecte "la population-disque" (le "blanc") et non la population "halo", c'est à dire le "jaune" qui, lui, ne tourne pas. L'image fossile de la galaxie est l'ensemble des 500 amas globulaires qui est ... statique affecte une forme sphéroïdale. Selon cette idée le halo de gaz et de poussières se constituerait assez vite en disque plat (en structure toroïdale qui se dégonfle au fur et à mesure quelle perd de l'énergie par rayonnement, ce qui est également simulable). Tout cela constitue un Meccano cosmique assez passionnant.

J'en profite pour dire aux fabriquants de galaxies en 2d eou en 3d qu'un modèle à deux populations, simple, consiste à associer un grumeau central qui ne tourne pas, où les forces de gravité sont équilibrées par les forces de pression et qui représente 90 % de la masse visible, avec un disque de gaz qui, lui, tourne. Ils retrouveront au passage la forme des courbes de rotation, avec des survitesses périphériques rendues possibles par la présence de matière gémellaire répulsive à proximité.

Une autre remarque à propos des simulations 2d, sur sphère. Certains, dans les "expériences de calcul" voient la matière gémellaire, confinante, se rassembler aux antipodes de la galaxie, sur la sphère S2. C'est parce qu'elle n'est pas assez "chaude" et que sa distance de Jeans 2d est plus petite que le périmètre de la sphère. Accroissez la vitesse d'agitation dans cette population et vous la verrez se répandre sur la sphère en constituant une nappe de densité quasi constante jusqu'à la "lacune" à l'intérieur de laquelle la galaxie viendra se loger (en 3d, dans un "trou dans du gruyère).

On pourra, avec ces planétoïdes numériques simuler la dislocation d'objets par effet de marée, au cours d'un passage dans la limite de Roche d'une planète. Théorie élémentaire , mais largement suffisante à ce lien. C'est simple à comprendre, mais le voir doit aussi être assez joli. On ne sait pas quel est l'âge des anneaux de Saturne, ni si ce sont des structures qui se sont constituées il y a un milliard d'années ou il y a mille ans seulement. . Tout ce qu'on sait c'est que leur limite extérieure correspond à la limite de Roche de la planète (2,5 fois son rayon). En bombardant Saturne avec des objets fragmentables (le modèle suggéré) on pourrait voir se constituer les anneaux de Saturne.

Pourquoi ne pas aussi faire se rencontrer la Terre avec un objet de la taille de Mars et simuler la naissance de la Lune ? Ca commence à se faire, mais la technique du calcul partagé permet de faire jeu égal avec les pros, voire même de les laisser loin derrière, si on a de meilleures idées.

En jouant avec tout cela on pourra faire émerger différents scénarios de constitution du système solaire. Mais ce qui est intéressant c'est de reconstituer son état actuel. En effet, selon Souriau, cet ensemble s'est configuré, de facto, pour devenir "le moins résonant possible" (sinon il évoluerait). Sous la non-résonance, les nombres irrationnels, à commencer par le plus irrationnel d'entre tous, le nombre d'or.

En analysant le système solaire en termes de non-résonance et en excluant le couple Neptune-Pluton, qui semble jouer à un autre jouer (c'est un couple au contraire très "résonant"), Souriau a fait apparaître la distribution correspondant à la courbe ci-après :

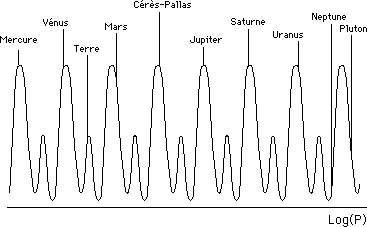
Les prédiction, correspondant à une "loi Dorée" collent assez bien. w étant le nombre d'or

Les rayons des orbites s'inscrivent alors selon une progression géométrique dont la raison est :

1,9ⁿ

Ci-après les deux courbes : loi de Bode et loi Dorée. La loi de Bode étant :

2,4 ( 0,4 + 0,3 2ⁿ)

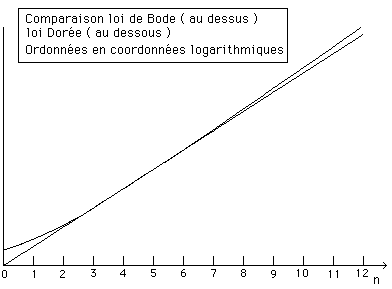
Comparaison des deux lois donnant les
rayons des orbites (en coordonnées logarithmiques)

Il y a donc un travail à faire pour montrer pourquoi et comment le système planétaire aurait pu évoluer de manière à s'ajuster selon la " Loi Dorée " de Souriau. Au cas où des gens seraient intéressés par l'aventure, Souriau serait a priori d'accord pour piloter ce genre de travail. Je lui ai posé la question.

Le système solaire pose des masses de problèmes :

- Pourquoi l'axe de rotation d'Uranus est-il couché au point d'être... dans le plan de l'écliptique ?

- Pourquoi Vénus tourne-t-elle "à l'envers" ?

- Pourquoi le couple Neptune-Pluton est-il "résonant" ?

- Etc....

Simulation de la précession des équinoxes :

- Masse de la Terre : 6 10²⁴ kilos
- Rayon : 6,4 10⁶ m
- Vitesse à l'équateur : 465 m/s

- MRV : 1,78 10³⁴

Encore une fois, j'ai la flemme de recalculer le moment cinétique d'une sphère de densité constante. Il y aura bien un lecteur pour m'aider &&&

- Masse de la Lune : 7,34 10²² kilos
- Distance à la Terre : 3,84 10⁸ m
- Vitesse orbitale : 1034 m/s

- Moment cinétique MRV : 2,88 10³⁴

Le "MRV" Terrestre est une limite supérieure. Il y a un coef devant de je ne sais plus combien. Toujours est-il que la majorité du moment cinétique de l'ensemble Terre-Lune est détenu par le satellite. Voilà encore une chose qui pourrait être éclaircie à l'aide d'une simulation 3d. Une autre simulation montrerait également que c'est la Lune qui tend à redresser l'axe de rotation de la Terre pour le rendre perpendiculaire à son plan d'orbitation.

Quand une toupie se couche sur une table, son axe de rotation subit un mouvement de précession. Là c'est aussi un mouvement de précession, lié au redressement de l'axe de rotation de la Terre. Tout s'amortit du fait des processus dissipatifs. Peut-on évaluer le temps au bout duquel l'axe de rotation de la terre se situera bien perpendiculairement au plan d'orbitation de Lune ?

Eclatez-vous : simulez la fin du monde :

Je ne considère comme pas du tout impossible que lors de la création du système solaire un astre de bonne taille, disons 4 fois la taille de la Terre, ait pu être placé sur une orbite très elliptique et dans un plan assez différent du plan de l'écliptique, par simple effet de fronde (rencontre rapprochée avec une planète géante). Si ceci produit un astre dont la période soit de plusieurs milliers d'années, celui-ci ne séjourne pas assez souvent dans le système solaire pour "s'assagir" en interagissant avec les autres planètes par effet de marée (résonateur : le Soleil). Son orbite pourrait ainsi se maintenir ainsi très en dehors du plan de l'écliptique et ne se serait pas circularisée.

Absurde, diront les astronomes. Un tel objet, on l'aurait observé ! Non, si en passant assez près de la planète géante qui l'a expédiée dans les confins par effet de fronde il a au passage pénétré dans sa "sphère de Roche". Alors ça ne serait pas une planète qui viendrait de temps à autre mettre un joli désordre dans notre système solaire mais une belle poignée de gravier, mêlée à des grélons de bonne taille. De temps à autre ce dangereux essaim nous frôlerait à des distances variables. Qu'un de ces caillous ou glaçons percuterait un continent et nous voilà renvoyé à l'ère des dinosaures avec un hiver nucléaire de 18 mois (le temps que mettent des particules d'un micron de diamètre de redescendre de la stratosphère où l'impact les aurait expédiées. Si l'objet tombe dans la mer, c'est un moindre mal. L'énergie crée une couverture nuageuse gigantesque. Comme dans les cumulus la privation de lumière refroidit la base du nuage, la vapeur d'eau se rassemble en gouttes et il pleut... 40 jours et quarante nuits.

Avez vous remarqué qu'on voit passer de plus en plus d'astéroïdes près de la Terre et de plus en plus près. Seraient-ce des "précurseurs", des blocs éparpillés le long d'une orbite que nous pourrions croiser un de ces quatre ?

Retour vers l'archive Projet Epistemotron