|
|
|
About this capture | ||||||||||||||
Problème des conditions aux limites
Calculs 2d sur une sphère S2
11 mai 2004
Nous avons vu dans le dossier précédent que se posait d'emblée un problème de conditions aux limites. L'univers n'est pas infini. Plusieurs solutions peuvent être envisagées. Nous avons vu que le fait de replier l'espace sur lui-même selon un "tore euclidien", équivalant à paver l'espace de manière périodique engendrait un artefact. Olivier Le Roy a utilisé un système simple, en 3d. Il a fait rebondir les points-masses sur les parois (immatérielles) d'un cube et obtenu ceci :

Simulation réalisée par Olivier Le Roy, printemps
2004
avec rebond des points-masses sur les parois d'un cube.
Nous avons imaginé de refermer un espace 2d selon une sphère S2, plongée dans un espace euclidien R3. On imagine que les points-masses glissent à la surface de cette sphère et s'attirent, ou se repoussent, selon une loi de Newton où on se sert de la distance curviligne, calculée le long d'une géodésique, c'est à dire du "grand cercle" passant par les points considérés. C'est beaucoup moins compliqué qu'il n'y paraît et plusieurs d'entre vous ont vite programmé cela. On calcule en fait dans R3. On commence par positionner les points sur la sphère, aléatoirement. Pour ce faire on dispose des points au hasard dans le cube à l'intérieur duquel la sphère peut être circonscrite (image D):
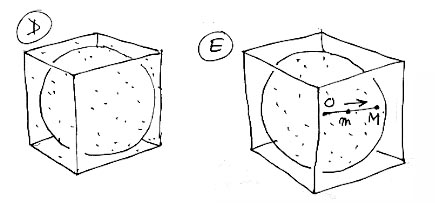
On élimine tous les points qui sont en dehors de la sphère, dont la distance au centre est supérieure au rayon, puis en divisant la distance radiale par le module du vecteur on amène tous les points sur la sphère (image E).
Pour fabriquer un vecteur tangent ayant une direction aléatoire on prend un vecteur unitaire U, partant du centre, ayant une direction quelconque, et on calcule le produit vectoriel :
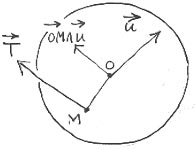
On peut alors porter un vecteur équipollent partant du point considéré de la sphère (vecteur T) et lui coller une vitesse, le module correspondant à une statistique de Maxwell-Boltzmann 2d :
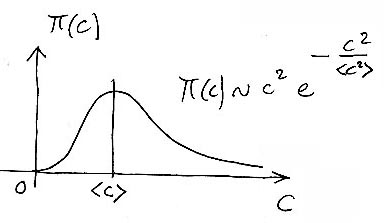
Statistique sur le module de la vitesse, distribution de Maxwell-Boltzmann
La distance curviligne se calcule à partir de l'angle indiqué :
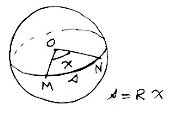
Distance curviligne sur géodésique (grande cercle)
On calcule ensuite la force d'attraction ou de répulsion qui se place sur un autre vecteur tangent de la sphère (tangent à la géodésique).
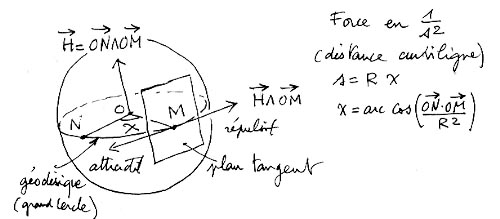
La "loi de Newton" dans un espace 2d fermé, sphérique.
On calcule la résultante de toutes les forces appliquées, qui est encore un vecteur situé dans le plan tangent à la sphère, là où se trouve le point-masse concerné. Reste à appliquer F = m G dans R3. Ceci va entraîner le point masse hors de la sphère. Ils suffit de le ramener dedans et de projeter son vecteur vitesse sur le plan tangent et le tour est joué.
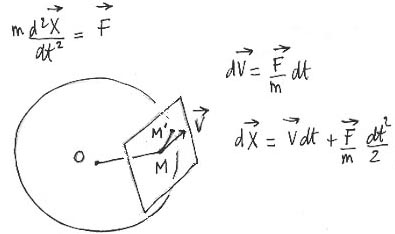
Je n'insiste pas parce que Gilles d'Agostini a composé un document où il explique tout cela avec sa clarté habituelle. C'est du Word. Vous pouvez cliquer dessus avec un clic à gauche ou avec un clicà droite en choisissant "Enregistrer la cible sous".
Gilles a créé un exécutable qui permettra à tout un chacun de faire lui-même des simulations "at home". Si vous obtenez des résultats, envoyez-les, si possible sous forme de gif animés qui ne pèsent pas trop lourd. Après avoir distribué par exemple des points de matière vous rechercherez les conditions où ce système commence à être instable, par instabilité gravitationnelle. Si rien n'apparaît c'est que les particules sont trop agitées (que ce gaz 2d est trop "chaud") ou que le milieu n'est pas assez dense. Voir le chapitre consacré à l'instabilité gravitationnelle. A justant les conditions vous obtiendrez votre premier grumeau ou cluster, dans un espace de calcul sphérique.

Il se formera ... n'importe où. Sur un des deux centres de rotation, diamétralement opposés si votre matière est animée d'un léger mouvement de giration. Gilles m'avait envoyé une jolie animation où on voyait cela mais je n'arrive pas à la retrouver dans le déluge de mails que je reçois quotidiennement. En principe la structure à grande échelle de l'univers découle d'un mélange où la matière gémellaire, étant plus dense (points-masses plus lourds) forme la première des clusters. La matière (la nôtre) est alors chassée dans l'espace interstitiel et donne cet aspect lacunaire que Landsheat et moi avions trouvé en 1992 (et publié en 1995 dans Astrophysics and Space Science). Voici à quoi cela devrait ressembler en 2d sphérique :
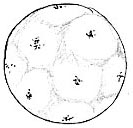
Et voici ce que nous avions obtenu en 1992 :

En 2d : la matière est confinée dans l'espace interstitiel en étant repoussée par les conglomérats de matière gémellaire
Ca, c'est du 2d. Il faudra un système à N ordinateurs pour refaire cela en 3d. Ca va être sacrément chouette. Savoir que cette structure devrait en principe se former quand l'univers est encore en expansion violente. Il faudra modéliser cette instabilité gravitationnelle dans un univers en expansion. J'indiquerai le moment venu comment il conviendra de procéder. Comme je l'ai expliqué dans l'ouvrage "On a perdu la moitié de l'univers" (1997) les conglomérats de matière gémellaire se forment les premiers. En effet, si les deux univers, le nôtre et le gémellaire, sont tous les deux en expansion, ils ne se détendent pas au même rythme. Ils n'ont pas "la même taille" pourtant ils sont "adjacents", "conjugués". C'est une idée un peu difficile à comprendre. En fait, nous sommes en plein mythe de la caverne, avec ... deux cavernes au lieu d'une. C'est du Platon-gémellaire. En fait les adverbes de lieu ne sont que des illusions commodes. Les "choses" ne sont nulle part en particulier. L'espace existe et n'existe pas. C'est une fiction mentale. Derrière cette vision gémellaire(qui cache en fait une structure à quatre feuillets, mais comme dirait Kipling, ceci est une autre histoire), c'est toute une refonte de notre conception de l'espace et du temps qui devra être effectuée. J'arrête pour ne pas embrouiller les esprits. Il y a des niveaux de réflexion où le cerveau devrait être équipé d'un disjoncteur.
On est obligé de se dire que "tout se passe comme si..."
On parle alors de "facteurs d'échelle" R et R*, la "jauge" R se référant à notre univers et et la jauge R* à son jumeau. Nous avons vu tout à l'heure qu'on pouvait calculer une distance curviligne à partir d'un angle c en écrivant simplement s = c R où R est le rayon de la sphère. En fait, tout point sur une sphère se définit par deux angles q et j (l'azimut et le site). La distance c aussi est un angle. Pouvez vous vous habituer, progressivement, à acquérir une conception angulaire de l'espace ? Quand nous opérerons dans une hypersphère S3 la position d'un point-masse dans cet espace dépendra non de deux angles, mais de trois. La distance aussi sera un angle. Pour avoir une distance métrique vous devrez multiplier cet angle par un facteur d'échelle R. A ce moment-là votre univers hypersphérique n'aura plus de centre. Pourtant, vous verrez que nous pourrons faire des calculs, en utilisant les quaternions.
Quand vous conjuguez des éléments empruntés à deux univers, le nôtre et son jumeau, pourriez-vous, en 2d, imaginer que ces taches de couleur que vous visualisez sur une seule sphère sont en fait une représentation mentale commode d'entités angulaires ? Deux angles, cela définit un rayon vecteur qui est comme un projecteur qui pointerait à partir du centre O, dans une direction de l'espace. Ce rayon vecteur produit deux taches sur deux sphères concentriques qui ont l'une un rayon R et l'autre un rayon R*. Une de ces sphère est notre univers et l'autre est ... son jumeau. Là, on commence à envisager que les facteurs d'échelles R et R* puissent différer, même si à chaque point M d'un des univers on peut associer un point conjugué M*. Ci-après une page de "On a perdu la moitié de l'Univers", Hachette collection Pluriel (à cette époque j'avais appelé la matière gémellaire la "matière-ombre" pour que ça fasse moins peur aux scientifiques. Mais ça n'a pas marché).
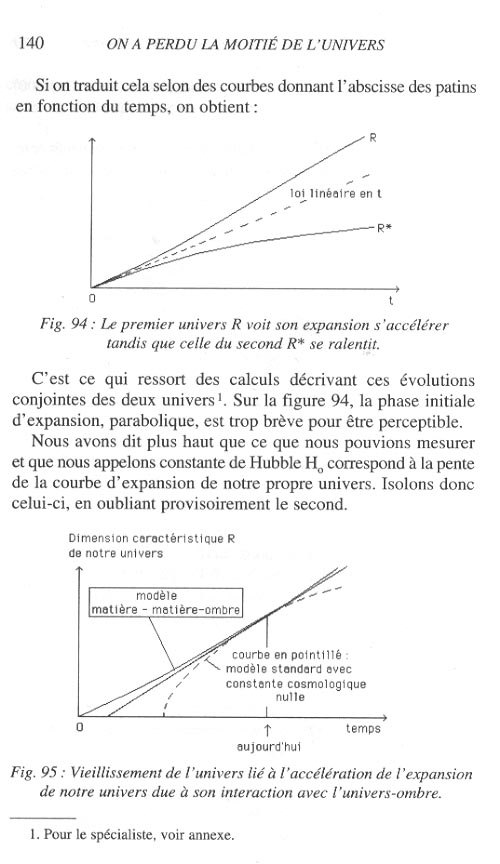
Un univers 2d en expansion c'est un ballon qui se gonfle. Là, il y a deux ballons, qui ne se gonflent pas de la même façon. Comme ces deux ballons sont faits de deux types de matière qui se repoussent mutuellement vous pouvez imaginer que si le ballon "gémellaire" a un rayon R* plus petit il puisse accroître le phénomène d'expansion d'un autre ballon, de rayon R, plus grand (où nous sommes censés habiter). C'est la raison de l'accélération "anormale" de notre propre univers. On interprète cela en disant que c'est l'effet "du pouvoir répulsif du vide". En fait il est simplement poussé au cul par sont jumeau. Phénomène inverse dans celui-ci. S'il était habité par des "astronomes gémellaires" ceux-ci observeraient un ralentissement de l'expansion qu'ils interpréteraient comme l'effet du "pouvoir attractif du vide".
Cette instabilité de ces expansions conjuguées fait que la matière, dans notre jumeau, est globalement plus dense. r* est plus élevé que r. Le temps de Jeans tj* est plus faible. Le jumeau forme donc ses conglomérats en premier. Les masses sont très importantes. Ces objets sont sphéroïdaux et constitués d'hydrogène et d'hélium "gémellaires". La physique du jumeau n'est pas fondamentalement différente de la nôtre (mais il y a probablement une violation inverse du principe de parité). Ces conglomérats peuvent être assimilés à d'immenses proto-étoiles qui... ne s'allumeront jamais. En effet la quantité de chaleur à évacuer croît comme le cube du rayon, alors que la surface rayonnante (en infrarouge) croît comme comme le carré. Le cooling time de ces proto-étoiles est grand devant l'âge de l'univers. Dans le jumeau "l'histoire" s'arrête là. Pas d'étoiles, pas de galaxies, pas d'éléments lourds, pas de vie. Seulement ces machins sphéroïdaux qui rayonnent dans le rouge et l'infrarouge. Dans le jumeau c'est :
Circulez, y a rien à voir
Dans notre univers les choses se passent différemment, et c'est là qu'on va déboucher sur une théorie de la formation des galaxies qui sera passionnante à explorer dans on pourra faire du full 3d. Les conglomérats se forment et repoussent la matière qui prend une allure de "bulles de savon jointives". Mais le phénomène, qui se produit quand l'univers connaît encore une expansion rapide, est brutal. La matière (de l'hydrogène et de l'hélium) est comprimé selon des plaques (les parois de "bulles de savon"). Cette géométrie est idéale pour qu'un refroidissement radiatif intense se produise. D'où une déstabilisation (voir le chapitre sur l'instabilité gravitationnelle). C'est à ce moment là que les galaxies se forment. Si vous faites le job, nous écrirons ensemble cette histoire là, pendant que les autres astrophysiciens continueront à jouer avec une matière sombre ou une énergie noire qui n'existent que dans leur imagination.
Quand j'essayais de publier dans Astronomy and Astrophysics le referee-grand-méchant-loup choisi par Lequeux me bombardait de questions.
- Si vous conglomérats de matière gémellaire existent, alors il doivent avoir un effet sur les images de objets situés à l'arrière plan.
Effectivement, comme ces objets se comportent comme des masses négatives ils créent, dans notre univers un effet de lentille gravitationnelle négatif. Ci-après les effets de lentille gravitationnelle positif et négatif, comparés.
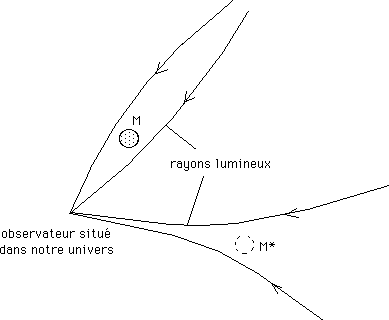
Effets de lentille gravitationnelle positif et négatif.
L'effet de lentille gravitationnelle négatif tend à réduire la magnitude apparente des objets situés à l'arrière-plan :

Or, qu'observe-t-on ? Les galaxies à fort redshift sont des "galaxies naines". Du moins c'est que pensent les astronomes, qui s'imaginent, sans donner de justification, que des galaxies de faibles masses se formeraient d'abord, pour s'assembler et donner ensuite des objets plus massifs. En fait ne nanisme est du à l'effet de "negative lensing". Mois après mois je répondais aux objections du referee de Lequeux et le papier s'allongeait, s'allongeait... Le jean James finit par tout stopper en précisant "que l'avis du referee n'était que consultatif".
Fermez le ban....
Vous comprenez pourquoi j'ai opté pour l'égyptologie (j'ai bien peur que chez les égyptologues ça ne se passe guère mieux. Mais au moins l'homme de la rue peut comprendre). Revenons à nos simulations sur sphère S2. Bien sûr; la structure spirale peut être créée en faisant interagir matière et matière gémellaire.

C'est ce qu'a commencé à faire Frédéric Baudemont. Quand il a vu ces images apparaître, il n'a pas dû en dormir de la nuit. Et ça ne fait que commencer. Attendez la féérie du 3d.
Le proverbe du jour :
Moins on est d'astrophysiciens, plus on rit
Dossier suivant :
Retour vers l'archive Projet Epistemotron