May JUN Jul 17 2003 2004 2005 1 capture 17 Jun 2004

About this capture

COLLECTED BY

Organization: Alexa Crawls

Starting in 1996, Alexa Internet has been donating their crawl data to the Internet Archive. Flowing in every day, these data are added to the Wayback Machine after an embargo period.

Collection: Alexa Crawl DX

Crawl DX from Alexa Internet. This data is currently not publicly accessible.

Une galaxie, c'est quoi ?

21 mai 2004

Depuis que des gens se sont attelés à ce projet EPISTEMOTRON, en obtenant parfois de très jolis résultats j'ai essayé de donner des indications, un fil conducteur. Il y a eu quelques notions indispensables de théorie cinétique des gaz. J'ai évoqué le mécanisme de l'instabilité gravitationnelle, le concept de longueur de Jeans. En procédant empiriquement, certains d'entre vous ont déjà pu reconstituer avec succès un certain nombre de choses que nous avions pu, Frédéric Landsheat et moi, faire émerger au début des années quatre-vingt dix. J'espère que quelqu'un pourra se charger de la définition du coefficient numérique qui se trouve dans la formule donnant la distance de Jeans 2d, ce qui permettra d'éviter des errances coûteuses en temps de calcul, et en temps tout court. En attendant que l'équipe qui se charge de faire travailler plusieurs ordinateurs ensemble ne puisse permettre d'envisager de gérer un million de points-masses en 3d, nous sommes confinés dans le 2d, avec des manips qui se font sur une sphère S2.

Sur cette sphère vous pouvez placer plusieurs populations de points-masses, avec des masses unitaires différentes, positives ou négatives, ainsi que des vitesses d'agitation thermique différentes.

Commençons par une première remarque. Il n'est pas nécessaire a priori d'introduire un spectre de masses. Les masses des étoiles sont relativement "centrées", la masse moyenne se trouvant être celle du Soleil (masse 2 10³⁰ kilos). Vous connaissez tous les chiffres. En dessous d'un dixième de masse solaire l'astre ne s'allume pas. Au delà de 10-20 masses solaires l'étoile termine une vie assez brève en devenant une supernova. Vis à vis de calculs ou de simulations cela n'apportera pas grand chose de plus de créer une distribution des masses avec une valeur moyenne et un écart-type. Cela compliquera plutôt.

A moins qu'en 3d quelqu'un ait envie d'étudier la dissipation d'un amas d'étoiles. Dans ce cas et dans ce cas-là seulement l'introduction d'une dispersion des masses est indispensable. Il faut alors créer un spectre des masses, de telle manière que les étoiles supermassives (masses limitées à 20 masses solaires) se comptent sur les doigts d'une main, qu'on trouve beaucoup d'étoiles de faibles masses (0,5 à 0,1 masse solaire), le reste étant à l'avenant.

En fait, tout cela est très spéculatif. Aucun astrophysicien ne serait capable de vous dire "l'amas d'où est issu le Soleil était composé de ...", tout simplement parce que personne n'était là pour les compter. Pour être plus précis, il y a dix ans beaucoup d'astrophysiciens croyaient que le Soleil était né "tout seul" et non dans un amas. Dans ce genre d'amas la masse moyenne et l'écart-type sont donc des paramètres relativement libres. Ce qui est intéressant à montrer ce sont les mécanismes. La configuration de l'amas, au moment de la fragmentation du nuage-pépinière est également très spéculative. Je pense personnellement que nos proto-étoiles devraient être "assez près" pour qu'en termes de théorie cinétique des gaz le régime soit dominé par les "collisions binaires" au départ. On peut modéliser différentes choses. Quand deux proto-étoiles étoiles de masses très dissemblables subissent une "collision frontale" (l'affaire étant gérée en terme de section efficace de collision) on pourrait envisager que la plus grosse absorbe la plus petite. Calculatoirement parlant, la petite étoile, de masse m, disparaîtrait et la grosse verrait sa masse passer de M à M + m .

Le second phénomène est l'accélération par effet de fronde, qui peut aussi s'interpréter comme une tendance à l'établissement d'un régime d'équilibre thermodynamique. Ainsi les étoiles massives accélèrent-elles les plus légères, au point de leur faire quitter l'amas (qui, perdant de la masse, voit sa dislocation s'accélérer). Tout le phénomène de l'instabilité de l'amas est intéressant à explorer, comme il sera intéressant, par la suite, d'étudier, avec un plus grand nombre de points-masses le comportement de proto-systèmes planétaires schématisés par un point-masse central - l'étoile - et un cocon de gaz de quelques milliers de points-masses tout autour. C'est "l'oeuf sur le plat 3d" avec le jaune au centre et le blanc autour. Ces oeufs se frôlent. La coque de poussières ( le "blanc" de l'oeuf) acquiert du moment cinétique, que conserveront pas la suite les étoiles géantes du système. Voir le dossier sur le système solaire. Etc... etc....

Revenons à des choses plus simples. En mettant des points-masses m sur une sphère, de même signe, le lecteur aura pu mettre en évidence le phénomène de l'instabilité gravitationnelle avec formation d'un ou de plusieurs clusters. Mais les choses intéressantes commencent quand on met sur la sphère deux fois N points-masses, avec des valeurs unitaires différentes. Bien que les expression du temps d'accrétion, de formation d'un cluster soient différentes en 2d et en 3d, voir le dossier, il reste que l'espèce qui possède la densité la plus importante (dont les points masses ont les valeurs les plus élevées) tend à donner des cluster la première. Il faut se placer dans ces conditions, de manière à voir apparaître, disons, une douzaine de clusters de cette espèce sur la sphère. Selon mon modèle il s'agira de matière gémellaire. Celle-ci, comme nous l'avions montré en 92 avec Frédéric Landsheat confine alors la seconde population, la matière, dans l'espace résiduel. On devrait pouvoir de nouveau resituer ces conditions et dégager ce pattern qui évoque, en 2d, la VLS, la Very Large Structure, la structure à grande échelle de l'univers où la matière s'assemble autour de vastes lacunes de 100 millions d'années lumière de diamètre.

Une précision : toutes les modélisations tentées pour reconstituer ce phénomène ont échoué, à commencer par le modèle "des crêpes, de Zel'dovitch". Personne, à part nous, n'a pu obtenir de structures stables. Au mieux les simulations menées à grand renfort de "matière sombre froide" fournissent-elles des structures vaguement filamenteuses, tenant plus de toiles d'araignées que de "bulles de savon jointive". Il y a un joli jackpot à gagner pour celui, ou ceux, qui réussiront à construire cette structure en 3d. Il y a gros à parier que les choses se passeront ainsi. Qui sait comment réagiront alors les astrophysiciens d'aujourd'hui ?

Au passage, une idée m'est venue. Après ma conférence au Collège de France, Jean-Claude Pecker, académicien et astrophysicien demandait pourquoi des astrophysiciens n'avaient pas tenté d'explorer cette voie. Je crois posséder la réponse. En fait, dans les labos, ces gens doivent travailler avec des logiciels tous faits, des boites noires. A l'intérieur de ces ensembles scellés tout a été soigneusement optimisé de longue date, le tree-code et tout le bazar. Il y a gros à parier qu'aucun de ce logiciels ne pose la question "définir le signe de la masse", pour une sous-population donnée. Pourquoi ces logiciels sont-ils "scellés" ? Parce qu'ils se vendent, pardi ! Pas question de fournir les sources. Je comprends au passage les réflexions des "simulateurs", interviewé dans Ciel et Espace. Ils ont des gros ordinateurs sur lesquels tournent des codes qu'ils n'ont eux-mêmes pas créés. Je comprends alors leur perplexité.

Venons-en aux galaxies. Je suppose que c'est ce qui intéressera le plus mes "savanturiers". Je vais d'abord dire quelques mots sur la structure d'une galaxie en 3d, puis évoquer ce qu'on pourrait faire en 2d. Une spirale représente 200 milliards de masses solaires, une elliptique dix fois plus. Les elliptiques sont en principe dépourvues de gaz. Quand elles ne tournent pas, ce sont des galaxies sphéroïdales. A un facteur d'échelle près elles sont alors structurées comme nos amas globulaires.

Amas globulaire ou galaxie sphéroïdale.

Tous les points lumineux qu'on voit sur ce cliché ne sont pas que des étoiles liées à cet amas. Il y a aussi des étoiles de la galaxie qui sont sur la "ligne de vue". Quand le 3d sera à portée de main il sera intéressant de recréer les galaxies elliptiques en introduisant un léger mouvement de rotation. Pourquoi ces elliptiques sont elles dépourvues de gaz ? Certains pensent que ces galaxies auraient pu se rentrer dedans dans leur prime jeunesse. On sait que les ensembles stellaires constituent des systèmes non-collisionnels. Ainsi deux galaxies peuvent-elles se passer au travers sans dommages, un peu comme deux nuages de moustiques venant à la rencontre l'un de l'autre. Mais le gaz forme un ensemble collisionnel. Ainsi, disent certains, la collision entre les deux masses de gaz interstellaire aurait provoqué, à travers son échauffement, la dispersion des atomes dans l'amas de galaxies. Pour qu'ils se dispersent il suffit que leur température absolue aille avec une vitesse d'agitation thermique excédant la vitesse de libération calculée à l'aide de la masse M de la galaxie (la faiblesse de cette théorie est qu'elle n'explique pas pourquoi les spirales, moins massives, auraient échappé à cette perte de leur gaz par collisions).

Un mot à propos du gaz interstellaire. Constitué essentiellement d'hydrogène, d'hélium, puis des ingrédients moléculaires (dont la présence est signalée par la façon dont ces molécules réagissent à l'irradiation stellaire) ces masses floues se déplacent l'une par rapport à l'autre à une vitesse de l'ordre du kilomètre par seconde. Une remarque achoppant avec la longueur de Jeans. Ces nuages correspondent à une certaine valeur moyenne de la densité r_g. En associant cette vitesse chamelière de déplacement et cette densité on retrouvera l'épaisseur de la couche de gaz, assimilée à la distance de Jeans dans ce macro-milieu

A l'intérieur de ces masses de gaz les atomes ont leur propre vitesse d'agitation thermique. Rappelez-vous la formule :

Introduisez la masse d'un atome d'hydrogène : 1,67 10^-27 kilo et la valeur de la constante de Boltzmann : k = 1,30 10^-23 vous obtenez la vitesse d'agitation de l'atome d'hydrogène en fonction de la température. En dessous de 3000° K il faut doubler la masse car il est à l'état moléculaire.

J'ai dit que les nuages dérivaient les uns par rapport aux autres à une vitesse de l'ordre de 1 km/s. Identifions cette vitesse à celle d'une vitesse d'agitation de l'hydrogène dans ces nuages. Nous trouvons 100° K. Ces pépinières d'étoiles sont assez froides, sauf quand ces mêmes atomes sont chauffés par des étoiles (mais ces échauffements locaux sont monnaie courante). De toute façon, en dehors de ces chauffages locaux, la vitesse d'agitation thermique dans les nuages et de l'ordre du km/s. C'est aussi la vitesse du ... son (qui est, selon la théorie cinétique des gaz, proche de la vitesse d'agitation thermique du milieu).

Tout le monde sait que quand on bouscule un gaz en y introduisant une perturbation (un objet comme un avion) qui se meut à une vitesse supérieure à celle du son il réagit en donnant naissance à des ondes de choc. Un kilomètre par seconde, c'est très peu. La perturbation constituée par la structure spirale des galaxies se propage dans le gaz interstellaire à une vitesse grandement supérieure. Aussi cette structure est-elle accompagnée par un phénomène d'onde de choc dans le gaz interstellaire. Celle-ci se trouve dans la concavité des bras spiraux. En ce lieu le gaz interstellaire se trouve "fortement recomprimé" (tout est relatif). Cette recompression s'accompagne d'une perte radiative. Le milieu s'en trouve déséquilibré et l'instabilité gravitationnelle produit de nouvelles étoiles, lesquelles, en émettant de l'UV s'empressent de contrarier le phénomène en réchauffant le gaz, en stabilisant le milieu, vis à vis de cette instabilité gravitationnelle. Phénomène homéostatique. On voit à travers ces images combien une galaxie est "vivante", comme elle "réagit" à l'apparition "d'ondes de densité". Bien sûr, nos simulations ne mettront pas en évidence cette naissance d'étoiles. Mais la structure de choc, peut être, si nous pouvons un jour gérer assez de points.

J'avais fait un dessin montrant cette structure d'onde de choc dans la partie de ma thèse consacrée à l'astrophysique, en 1974. Mais je n'ai plus ce document sous la main. Je ferai une remarque. Avez vous observé une baignoire en train de se vider ? Il faut être attentif car le phénomène est relativement bref. L'eau s'engouffre en spiralant dans la bonde. Quand le niveau de l'eau baisse des vagues spiralées apparaissent. Elles sont l'analogue de ces ondes de choc, tout simplement parce que la vitesse de circulation quasi-circulaire dépasse alors l'équivalent de la vitesse du son, c'est à dire celle de la propagation des ondes de surface.

Dans quel sens tournent ces ondes spirales ?

Messieurs, à vos baignoires...

Si vous allez un jour au Kenya-Tanzanie, en partant de Nairobi et en descendant vers le sud vous franchirez l'équateur. Ca n'a rien de particulièrement spectaculaire. Contrairement à ce qui figure sur les mappemondes il n'y a rien d'écrit, pas de ligne équatoriale. C'est une plaine très banale. Mais (du moins du temps où j'étais guide de safari, là-bas) on trouvait gars avec deux cuvettes, munies d'un trou et fermées par un bouchon. En principe la force de Coriolis devait faire en sorte que le sens de rotation de l'eau, dans la bonde, s'inverse. Bien sûr, on ne voyait rien. Mais je me demande quel était l'olibrius qui avait monté cette manip dans un endroit pareil. Il est vrai qu'en Afrique on tombe souvent sur des choses étonnantes. Il faudra que j'écrive un livre là-dessus.

J'avais intitulé ce dossier : "Une galaxie, c'est quoi ?" et je vois que j'ai fait pas mal de digressions. On peut schématiser une galaxie spirale par deux populations.

- Le "gaz d'étoiles"

- Le gaz interstellaire.

Je vous ai déjà parlé des amas globulaires. Il y en a 500 dans notre galaxie, qui forment un ensemble à symétrie sphérique. Dont cet ensemble ne tourne pas. Il est également insensible à ces vagues que constituent la structure spirale qui affecte le gaz interstellaire, pas, ou très peu la population des étoiles. Il sera donc possible de schématiser une galaxie à l'aide de deux populations. Quand on fera du 3d on créera cette "population halo" à symétrie quasi sphéroïdale en partant d'une solution analytique (solution elliptique du tandem équation de Vlasov, équation de Poisson). On pourra ensuite surajouter une crêpe de gaz, dont le bord externe viendra interagir avec une "frontière invisible" constituée de matière gémellaire. On obtiendra alors une structure spirale stable, ce que les autres astrophysiciens ne parviennent pas à faire. Les galaxies d'Athanassoula ont perdu leurs bras pendant des décennies. Françoise Combes s'est amusée pendant quelques années à jeter des pelletées d'hydrogène froid dans une galaxie constituée d'étoiles en rotation. Ca spiralait gentiment, mais ça ne durait pas. De plus on n'a jamais observé ces masses d'hydrogène froid auxquelles dame Combes prête la vertu de créer ces formations spirales. Elle ne les trouvera jamais, tout simplement parce que le gaz qui se trouve entre les galaxie est chaud. Il émet même dans la gamme de X.

Dans une vie de chercheur on ne trouve souvent guère plus d'une idée. Athanassoula a vieilli en regardant ses galaxies se transformer en cacahuètes tournantes, après avoir vu leurs jolis bras spiraux s'évaporer. Françoise Combes s'achemine vers la retraite, lasse de jeter dans ses galaxies des pelletées d'hydrogène froid qui n'ont jamais existé que dans son imagination. C'est dur, la vie de chercheur, quand on n'a pas d'idées de rechange.

Je pense à un de mes vieux amis, que je ne citerai pas et qui ne m'en voudra pas de le taquiner ainsi. Vous savez qu'un des candidats pour la matière sombre étaient ces "MACHOs" (Massive Compact Halo Objects). Autrement dit des gros Jupiter. On monta il y a 15 ans un programme ambitieux pour les détecter. Pour ce faire on utilisait "des télescopes à grand champ" enregistrant mois après mois la lumière émise par des myriades d'étoiles. Pour éviter les perturbation liée à un présence de trop de paquets de gaz interstellaire on visa une galaxie satellite de la nôtre : le Nuage de Magellan. Selon les calculs des occultations partielles d'étoiles devaient se produire quand un macho passait entre celle-ci et l'observateur. Il y avait donc une baisse de luminosité, que l'analyse du cliché par ordinateur permettait de détecter. Il y avait alors deux possibilités :

- Ou la baisse de lumière ne se reproduisait pas et il pouvait effectivement s'agir d'un macho

- Ou elle s'inscrivait dans une périodicité et c'était alors soit une étoile associée à un compagnon, soit une étoile variable.

On attendit dix ans. On multiplia les missions au Chili. Et ... que dalles. Rien que des étoiles variables ou des systèmes binaires. Mon ami était désespéré...

Revenons à nos astro-moutons. En 3d une galaxie assez acceptable c'est un ensemble sphéroïdal plus un disque de gaz. Mais nous n'en sommes pas encore là. Nous sommes toujours dans le 2d. A mon avis la structure spirale se forme en même temps que la galaxie elle-même. Mais ça, ça serait un plus difficile à simuler car il faudra calculer ... sur une sphère qui se gonfle. Remettons cela à plus tard (En 3d nous ferons croître le volume d'une hypersphère S3).

Quand vous faites des simulations avec une seule population, si vous introduisez un léger mouvement de rotation le cluster va se former au voisinage de l'axe de rotation (l'un des deux pôles, si les conditions sont bien choisies). Ce que je suggère c'est que vous preniez de la matière gémellaire "chaude", stable, non susceptible de forme des clusters, parce que sa longueur de Jeans 2d sera supérieure au périmètre de la sphère, et une densité uniforme de matière, en rotation. Celle-ci se transformera en galaxie, en conservant son moment cinétique. Alors cette seconde population donnera une formation spirale. Mais il ne s'agira pas de la simulation 2d la plus fidèle d'une galaxie. Il faudrait deux populations.

Comment faire ?

- Faire une première expérience de calcul avec deux populations, sans mouvement de rotation. Vous obtiendrez alors un cluster immobile, ou quasi immobile.

- il faudrait alors rajouter le gaz.

Cela ferait trois populations, avec un nombre limité de points. Mais on pourrait ruser en se disant que la population halo (d'étoiles) qui représente 90 % de la masse de la galaxie est relativement peu sensible au phénomène de l'onde de densité spirale. On pourrait alors calculer le champ gravitationnel créé par le cluster. Il serait éventuellement possible de le fixe en "clouant" une bonne masse en son centre, clouée sur la sphère S2. Puis, dans ce champ de potentiel, cette force en 1 sur s puissance quelque chose (s représentant la distance curviligne au centre géométrique du système) on colle un disque de gaz qui tourne en corps solide. On récupère alors ces points de matière, censés représenter des étoiles, pour en faire des "points-gaz". En on laisse aller. Moi, c'est ce que je ferai.

Tout cela c'est en attendant le calcul parallèle, qui décuplera le nombre des points et permettra, d'abord en 2d puis en 3d, de serrer au plus près les phénomènes. Plus nous aurons de points masses et plus nous pourrons modéliser les phénomènes.

Attention, espace courbe !

Une dernière remarque : certains présentent sur l'écran de l'ordinateur la demi sphère visible, complète. Et, dans cette demi-sphère la galaxie occupe une aire non négligeable. Or dites-vous bien que cette géométrie sphérique n'est là que pour fermer l'espace, pour escamoter le problèmes des conditions aux limites. Mais en opérant ainsi nous travaillons dans un espace courbe. Pour bien faire il faudrait que la galaxie ne s'étende pas sur plus du dixième du diamètre de la sphère. Alors, là où elle s'ébat, l'espace est quasi-plat. En 3d on fera pareil et on raisonnera alors en terme de volumes.

Mon ami Gilles d'Agostini a créé son propre programme avec lequel il a déjà pas mal joué. Il a en particulier mis au centre de son écran, au centre du cercle-contour apparent figurant sa sphère un solide point masse, fixe. Puis il a fait orbiter autour de celui-ci un point matériel plus léger, en espérant pouvoir retrouver les orbites Képlériennes. En étendant cette trajectoire quasi-elliptique sur une bonne partie de la sphère voici ce qu'il a obtenu :

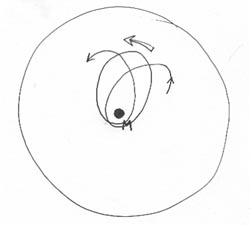
Précession du périhélie

Gilles a cru à une erreur de calcul, à un pas trop grand. Mais non : Newton, sur du courbe, ça donne des ellipse qui précessionnent. C'est ce que fait ... Mercure. On peut calculer les trajectoires relativistes exactes et je vous le ferai faire un jour. C'est rien du tout. J'avais fait tourner cela il y a vingt ans sur un Amstrad 6128. On obtient alors la précession des ellipses et l'effet de lentille gravitationnelle. Ca permettra d'approcher de plus près la question des étoiles à neutrons, à travers des simulations relativistes (dites-vous bien que si vous me suivez dans cette voie pendant quelque temps, après, votre mère ne vous reconnaîtra plus).

Pour le moment, essayons de nous affranchir de cet effet de courbure qui ne fait que parasiter notre calcul. Moralité : si vous voulez simuler quelque chose en 2d, débrouillez vous pour que ça se passe dans un bout de sphère "pas trop grand", ce qui ne pourra se faire que quand on aura, grâce à un calcul parallèle avec seulement quelques machines, de quoi bien peupler en points tout ce qui est extérieur à notre zone de travail "quasi-plane", et qui sera peuplé de matière gémellaire.

Retour vers l'archive Projet Epistémotron